Injective functions – definition

Last post, I’ve looked at the definition of a function and how it matches up with we should expect from a function. Here, I’ll be looking at the different properties a function can have – the first is what it means to be injective.

We should start off by looking at the definition:

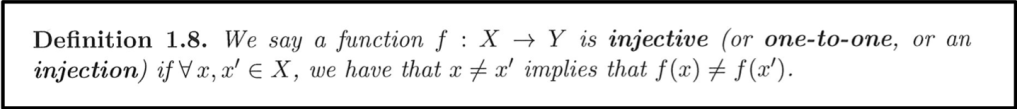
Right, we see that for a function f to be injective, some conditions have to be met.

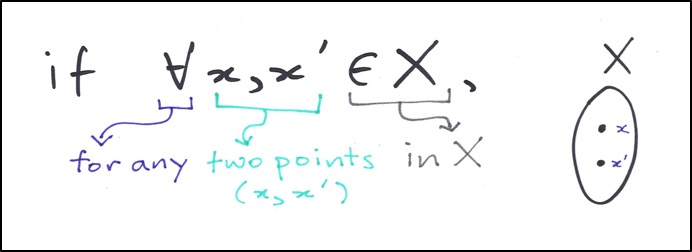
The first part seems simple enough: whatever follows next in the definition has to work for all possible pairs of points x and x’ in X. If we happen to come across a pair of points that fail, then the function cannot be injective.

OK, you know when I mentioned previously that reading maths is a skill that needs to be practiced? Well, the second part needs a little interpretation:

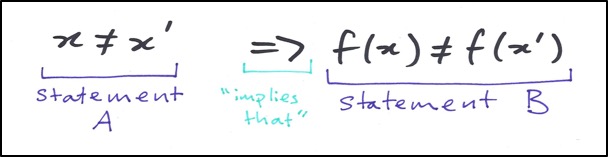
And this can be rewritten again:

So when you see the words “implies that” – or its symbol – you can interpret that as “if A is true, then B is also true”.

Remember, notation is not meant to be confusing. We could choose to write “x is equal to y”, but you’d probably agree that writing “x = y” is easier to write and is more concise.

So now, what does the second part of the definition mean? Let’s draw a diagram:

We see that that both x and x’ map onto the point y.  This means that y = f(x) and y = f(x’), and thus f(x) = f(x’). Hold on though, if we re-read the definition again…

This means that our function f doesn’t satisfy the condition in the definition and so f is not injective. If we re-draw our function:

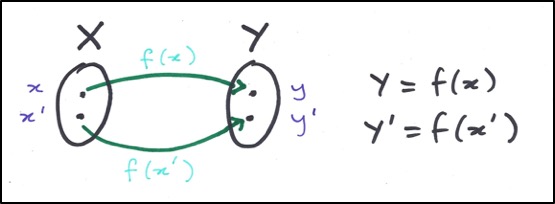
Here x and x’ map onto different points, y and y’ respectively. So f(x) ≠ f(x’) and the condition is met. We can now say that f is injective.

A few more examples:

Here is another function g that goes from A to B. If we take any two different numbers in A, we should end up with two different outputs in B. A quick check should confirm that this is correct, and thus g is injective.

Here I’ll leave this for you to figure out, but an easy way to find out if a function is not injective is to find two different points x and x’ that map onto the same y and thus the condition for injectivity cannot be met.

And finally, I’ll leave you with two last questions to think about:

• Why is an injective function also known as a one-to-one function?
• Can you break down the definition in the same way for a surjective function?